ブリルさんからの挑戦
数年前、折紙探偵団名古屋コンベンションのゲストとして来日されたデビッド・ブリルさんから出された問題。 食事を注文して出てくるまでの間の話題だったのだが、飲食中にもずっと考えていた折り紙バカが約1名いた。
解けたらBOS購読1年分をプレゼントだそうだ(酒の席での話です。念のため)。
問題
ブリルさんは馬(※1)を2体折ろうと考え、紙を買いに行きました。
ちょうど良い1:√2の紙を見つけましたが、残念ながら1枚しか在庫がありませんでした。
この1枚の1:√2の長方形から、馬を折るための2枚の正三角形を最大の大きさで、また正三角形の内部に無駄な折り筋がつかないように折り出すには、どのようにすれば良いのでしょうか?
美しい仕上がりのため、正三角形の中には折り筋をつけてはいけませんが、紙の辺につける最低限の印は許容範囲とします。
正確じゃないけれど、大体こんな感じの問題。
※1 ブリル氏の代表作の一つ。正三角形の用紙から折る、ブリル氏らしい美しい作品。
参考リンク:ブリル氏のウェブサイト
『端正な折り紙』に折り図が収録されています(画像はamazonリンク)。
折り出すための方法
1:√2の紙から2つの正三角形を作る場合、切り出し方は図1のような形になる。ちょっと考えると「無駄な折り筋がつかないように」という条件から、まずは中心を通る線を折り出さなければいけなさそうだ、ということが分かる。実質的には、この線をどう折り出すかという問題であると考えてよさそうだ。
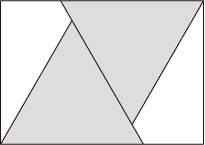
図1 2つの正三角形の切り出し配置。
面白いのは、シンプルな問題ながら、一般的に知られている正三角形の折り出し方法が使えない事だ。
その上で、不可能ではなさそうというのも想像できるという、とてもよくできた問題だ。
さて、どうする?
考えられる方法は、
1.正三角形以外の部分で30度を折り出し、それを使って点を折り出す
2.シルバー矩形の対角線の√3を利用する(※2)
3.中心点から、なんらかの形で60度の線を折り出す
あたりか。
無駄な折り筋をつけないという制約のため、どちらにしても一筋縄ではいかなさそうだ。
※2 √3が折り出せれば、正三角形も折りだせると考えて良い。√3自体は簡単に折り出せるが……
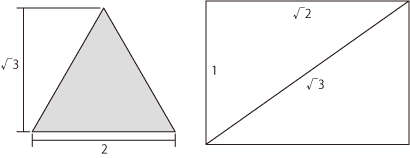
それぞれの方法を考えてみる
1.の場合、そもそも60度を折り出す方法が限られているのが問題になる。というのも、折り筋をつけられるスペースが限られているからだ(図3)。
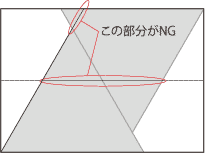
図3 一般的は60度の折り出しでは、余計な折り線がついてしまう。
一般的な60度の折り出しは使えないので、エレガントでは無いけれど、長方形のカドの部分でチマチマと60度を折り出して、それを大きくして行く方法で一応折り出す事ができそうだ(図4)。
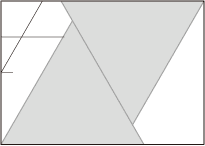
図4 切り出す三角形の外側の部分を使えば、とりあえず角度は折り出す事が出来る。ここから長さを写すようにしていけば、一応必要な点は折り出せる。
2.の場合、1と同様に基準に出来る線が少なすぎるのが問題となる。不可能ではなさそうだが、1の方法同様に小さく折り出して大きくしていく必要がありそうだ。なんにしても泥臭い解しか出てきそうに無い
意外な解
で、いろいろと考えていてふと思いついたのが3.、2つの点を同時に合わせる方法で、これを使うと必要な折り筋を直接折り出す事が出来る(図5)。
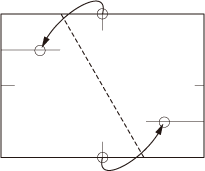
図5 実際にやってみると分かるが、表裏で合わせなければいけないので折りにくい。
実はこの方法、「2点p1, p2 2本の直線l1,l2が与えられたとき、p1をl1上に重ね、かつp2をl2上に重ねる」といういわゆる6番目の折り紙公理(※3)を使っている。
存在は知られているものの、実際にはほとんど使われない公理を使う意外性、つける折り筋の少なさ、また表裏で同時に基準点を合わせる実用性の無さまでも含めて、面白い解なのは間違いなさそうだ。
※3 紙を折るための操作の規則。7種類存在することが知られている。
参考リンク:K's 折り紙:紙による作図
Wikipedia 折り紙公理
……というのを
食事が終わる頃に見つけて、ブリルさんに報告できた。という事で、BOS購読権をゲット。おめでとう>私。
ちなみに、ブリルさんの用意していた答えは、近似値を使った折りやすい方法で、まさか力技(?)で解いてしまうとは思わなかったと呆れていた。
Q:で、これは何の役に立つのか?
A:シルバー矩形から馬を2体折る時に使えます。
まあ実用性はともかく、よい問題に対して面白い解が出せたのが、本人にとっては面白かったというのが重要なのです。
