ずいぶん前のコンベンションで宮島さんに聞かれてた問題。実は少し後に答え自体は出ていたのだけれど、放っておいて今に至る。
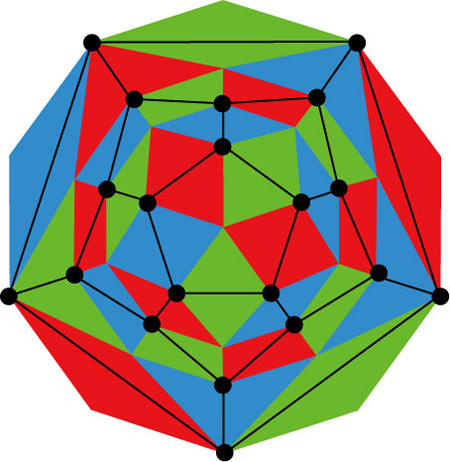
パターンの分析
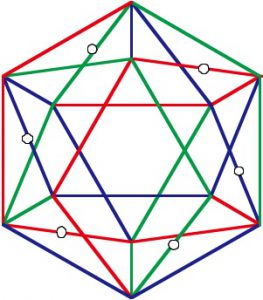
正20面体の辺の色分けと考えるのが、個人的にはやりやすいと思う。
まず思いついたのが、それぞれの色各10枚の位置関係は対称にはならない事。正多面体の対称性を考えると、いくつかの種類に別れるはず。10の対称”面”ならあるけれど、今回はあまり使えなさそう。
次に色分け図を見て気がついたのが、5本の辺がそれぞれ繋がっている事と、それが6本絡み合っている事。これはよく考えると当たり前の話で、各頂点には5本の辺が集まっているので、3色での色分けでは必ず1:2:2となる。この1が6本の色線の端になる。で、頂点は12なので色線は6本となる。
整理されてきた。 まず、6本3色であれば対称性が分かりやすい。正四面体の各辺だ。 さらに色分け図を詳しく見ると、5本の辺はS字に曲がっている事に気がつく。たしかにこれ以外では無理っぽい。正20面体=変形正四面体であると考えれば、納得の対称性と位置関係。という事で、構造的には右巻きと左巻きの2種類がある。
※印の辺が5本繋がっている中心の辺
具体的な組み方
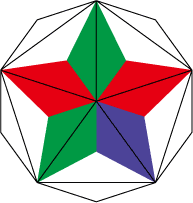
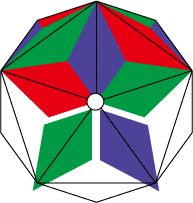
1. まず20面体の頂点5枚を組む。色はa(青)×1:b(赤)×2:c(緑)×2になる。
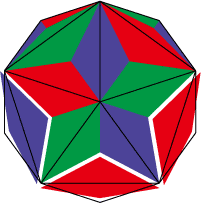
2. その周りを組んで三角形の面5つをつくる。これは自動的に決まる。使うのはa(青)×3:b(赤)×1:c(緑)×1。
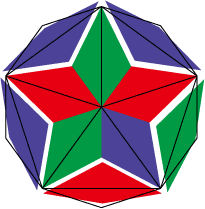
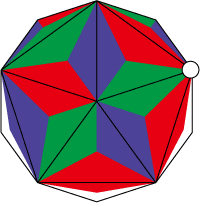
3. 手順1でa(青)を使っている頂点（白印）に注目、a(青)ともう１つ(b(赤)またはc(緑))を合わせて頂点をつくる。
印の頂点を手前にする。
a(青)ともう１つ(図ではc(緑))で頂点をつくる。
4. 3つ組み合わせて三角形の面3つをつくる。
5. 2カ所あるユニットが4つ集まっている頂点のうち、片方は両側の色が違うため確定している。3つ組み合わせて面を2つつくる。
4つのユニットが集まっている印の頂点を手前に。
色はc(緑)に確定している。両側も組み合わせる。
6. あとは確定している頂点・面を順番に埋めていけば完成。
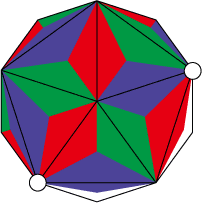印の頂点はつなぐパーツの色が確定済。それぞれ組んで進めていけば全体が組み上がる。
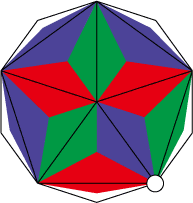
ポイントとなるのは3の手順で、ここで正しい色のパーツを組む事で巻き方向を確定、残りの色も全て決まります。逆にここで間違えて緑と赤を組んでしまうと、少し先で行き詰まります。線対称になっているので、2つ先くらいの手順で同じ色が隣り合うはず。
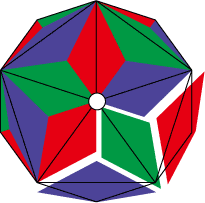
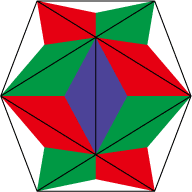これはダメなパターン。青のパーツが赤と緑で取り囲まれている。
