フラクタル図形コッホ雪片を、繰り返し可能な状態で折れたっぽいので情報を整理・出力しておきます。
形の捉え方と基本構造
今回折るのはコッホ雪片には、限られた繰り返し回数ではありますが池上牛雄氏の作例があります。この作例と池上氏の挑戦の軌跡をよくみてみると、凹部分に近い小さい角がどこから生えてくるのかというのが問題となっています。繰り返し可能な作品を目指すのであれば、おそらくこれを解決することが実現の鍵となるでしょう。
今回(実は10年以上前〜)、形から考えると行き詰まりそうなので、試しにカドの折り出しで形を作ることができないかを考えてみました。ただし、この場合でも同じように、中心に近い部分のカドをどう出すかが問題となります。直線のカドとして考えると、非常に中途半端な位置からカドを折り出す形になります(図1、図2)。
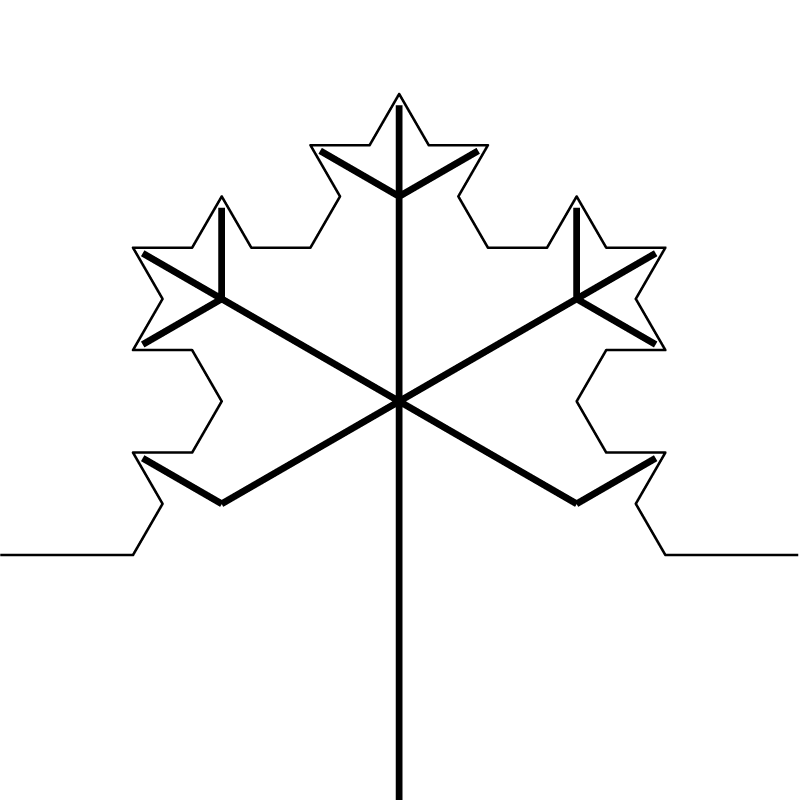
ここで少し考え方を変えてみます。折り紙作品ではカドは途中で曲げられるので、中心に近い部分から直線として折り出すより、外周に近いところから分岐させる方が実現しやすそうです(図3)。
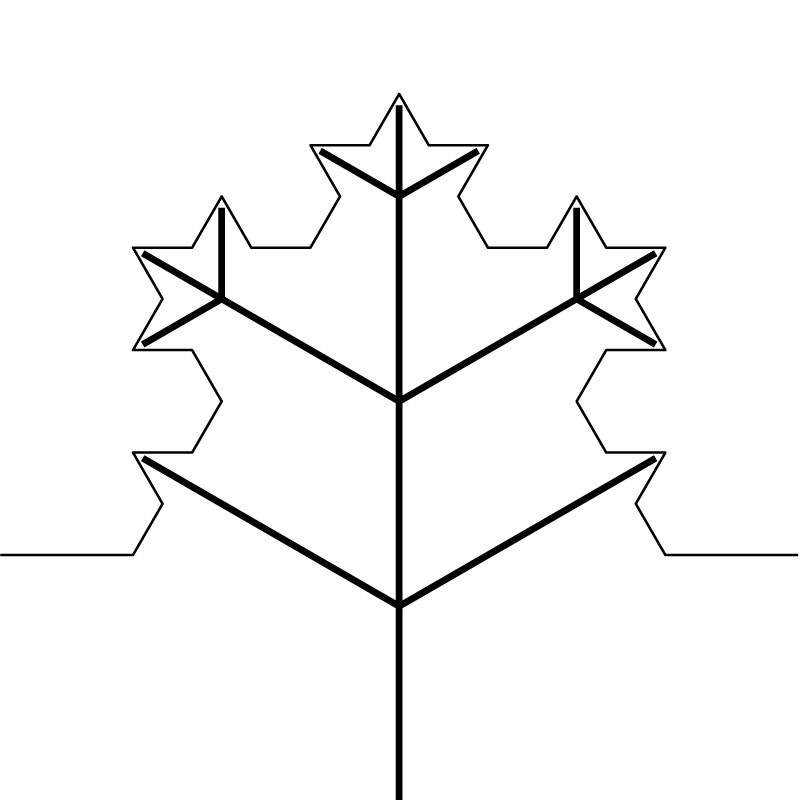
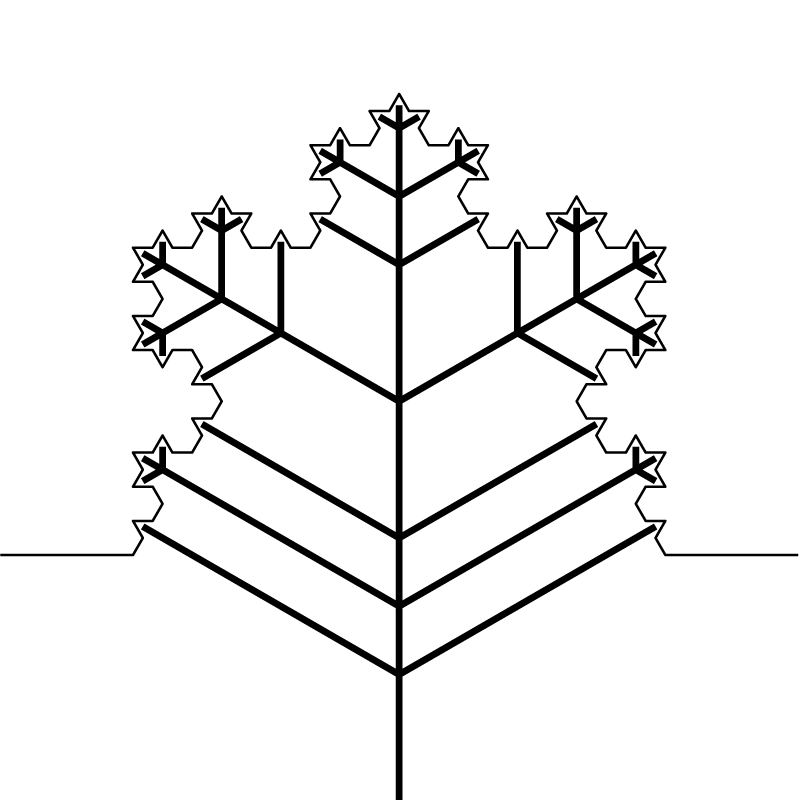
もう少し考えを進めて、それぞれのカドが5方向に分岐して、内側の部分は使わない構造と考えると、小さいカドを自然な階層構造に組み込むことができます(図4)。
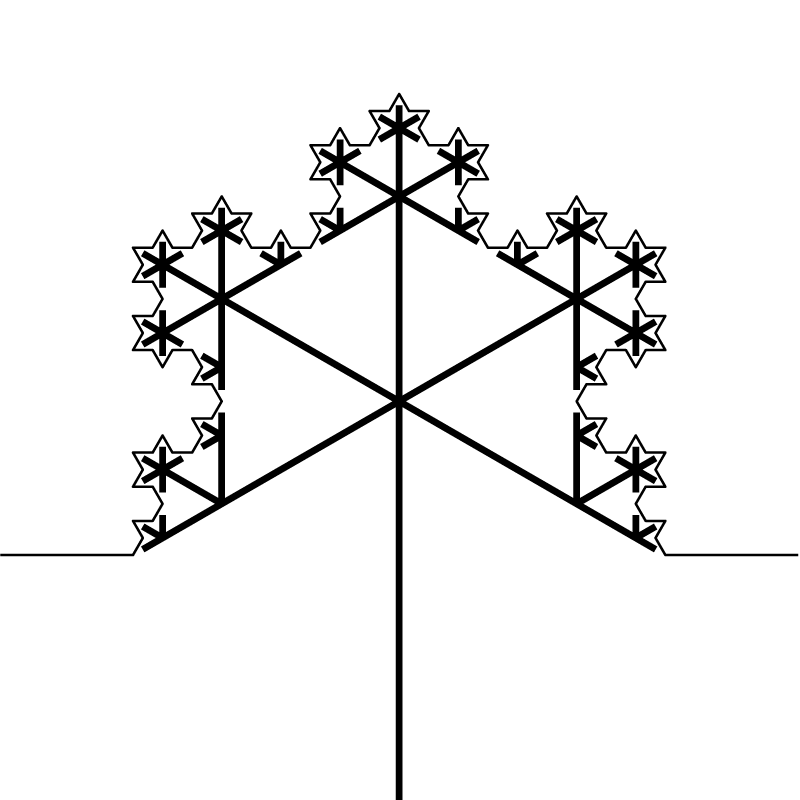
実際の形としては、カドではなく星形を折り出すことになります。1/3の大きさの星形を各角に重ねることで、結果的にコッホ雪片を折り出すことができる……はずです(図5)。
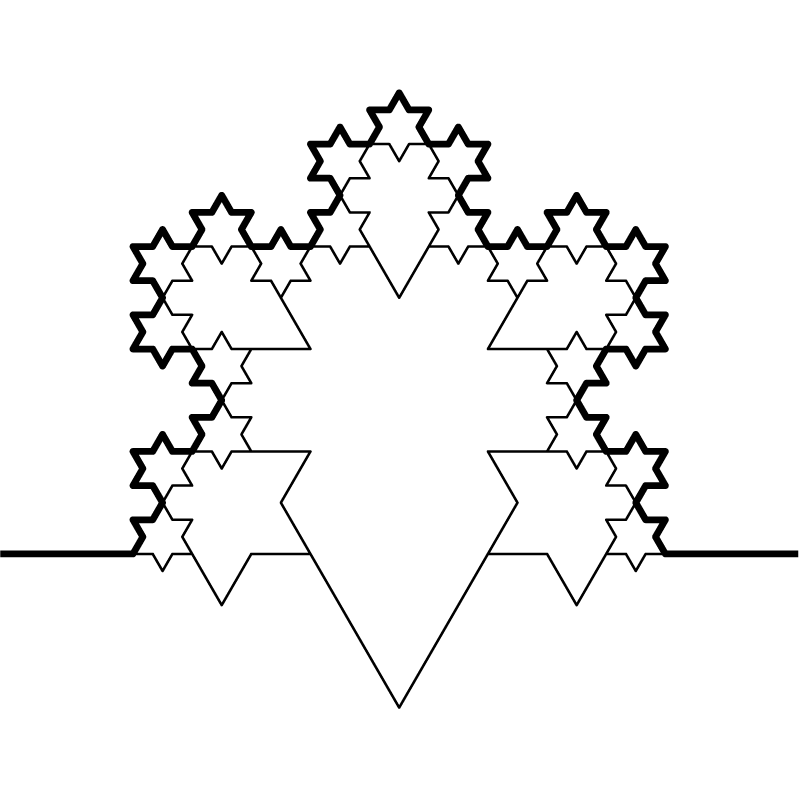
さて、この構造なのですが、実は池上氏のフラクタルピラミッドを6方向にしたものと同じような構造となります。さらに言えば、今回は図形の内側部分を作る必要がないため、実現までの難度は「異常に高くはない」ことが予想できます。これで「不可能ではなさそう」ということが見えてきました。それどころか、かなり再現可能性の高い、有望な方法のようです。それにしてもここで別のフラクタル作品とリンクするのは熱い。
基本的な構造
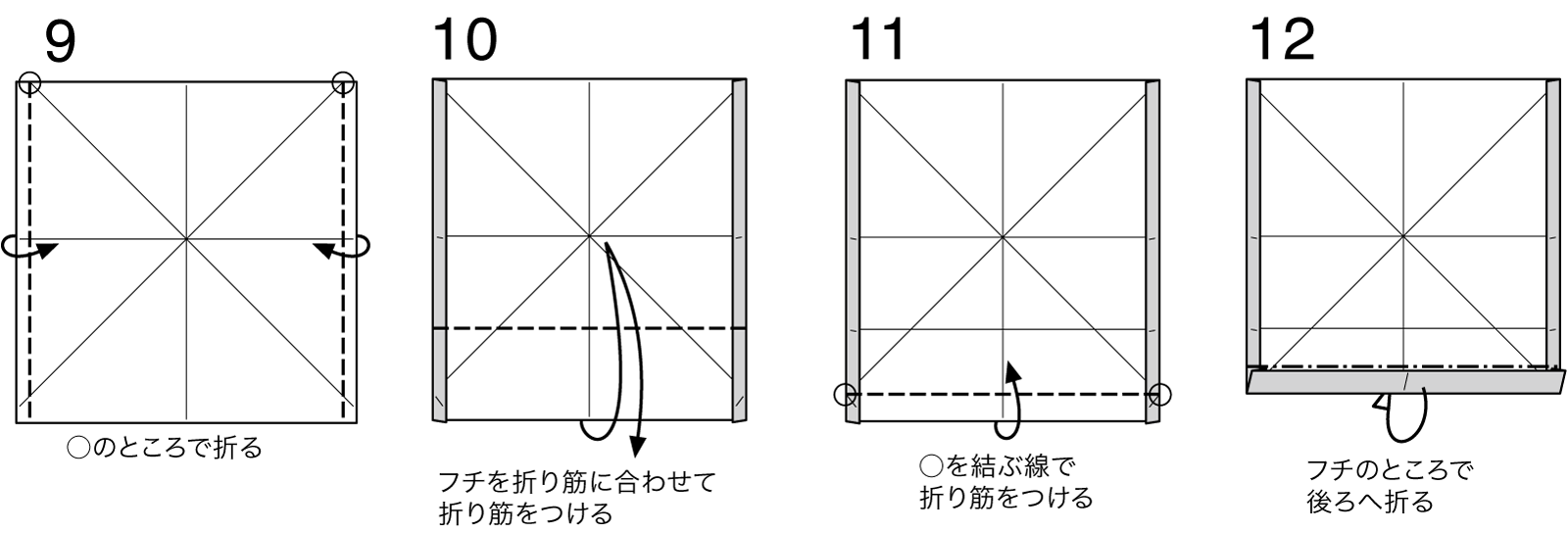
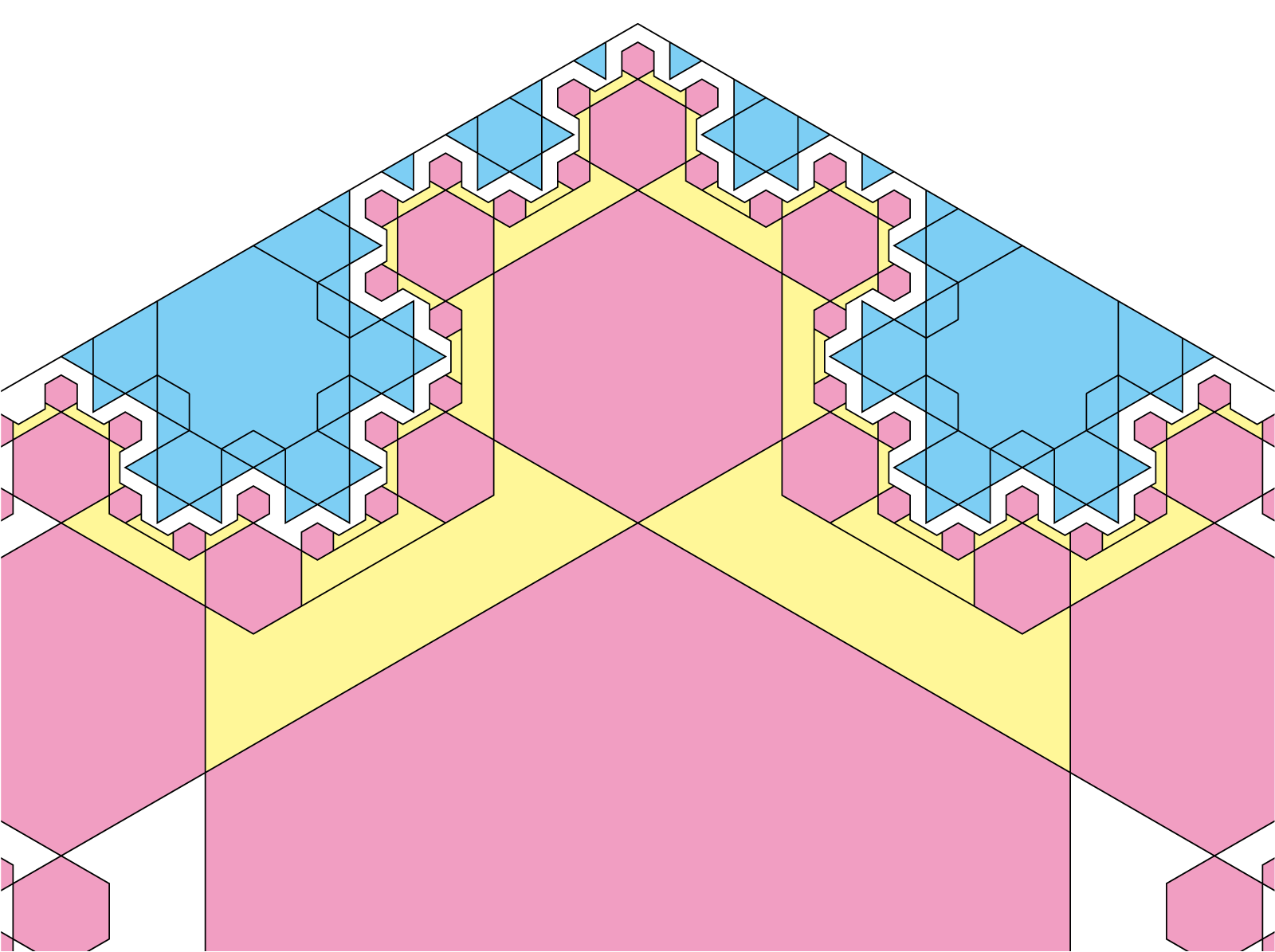
実際に折るための配置を考えてみます(これが数年前〜昨年)。まず各星形のパーツは、フラクタルピラミッドと同様にそれぞれのカドを合わせる配置でよさそうです。領域はとりあえず6角形で行います(マゼンダの六角形)。
次に、隙間を埋めるようにして構造を分けてみます。折紙探偵団マガジン88号で池上氏が提唱しているような階層化構造が成立するので、内側向きに関しては繰り返しが成立しそうです(イエローの台形のような形)。
外側については読みきれないのですが、階層構造は成立しそうだし、長さをみる限りは問題なさそうです。ここから先は現物で検証するのがよいでしょう(シアンのコッホ雪片状の部分)。
2023/12の試作と挑戦
ということで、大まかな構造も決まったので実際に折って試作してみました。まず星形部分の構造は、折りやすさ重視でもとの領域の1/2の大きさになるものを採用しました。最終的には元の用紙の1/4の大きさの完成形となります。細かい問題はあったものの、とりあえずではあるものの折り畳み出来そうというところまで進めることができました。
次に再度整理しながら試作します。3段階の状態で内側部分の折り畳みができました。上記構造図のイエロー部分が一つある段階で、フチの形状を見る限り繰り返しも可能です。外側は不安定ですが、とりあえず星形に削り切ることができました。ということで3段階目完了です。
次の階目に向けて
次の段階を折るために、確認すべき問題は2点。内側の繰り返しに問題がないか、そして外側の折り畳みです。まず内側については、まず間違いなく大丈夫そうです。ただ現物だと、紙の重なりなどの干渉で条件が変わる場合も考えられるので検証が必要でしょう。
また外側については、繰り返し回数が少ないこともあり、パターンが読みきれていません。ただ経験上の勘では「まず間違いなく可能」です。とにかく、この段階ができれば多分いくらでも先に進められそうです。
実際に折る
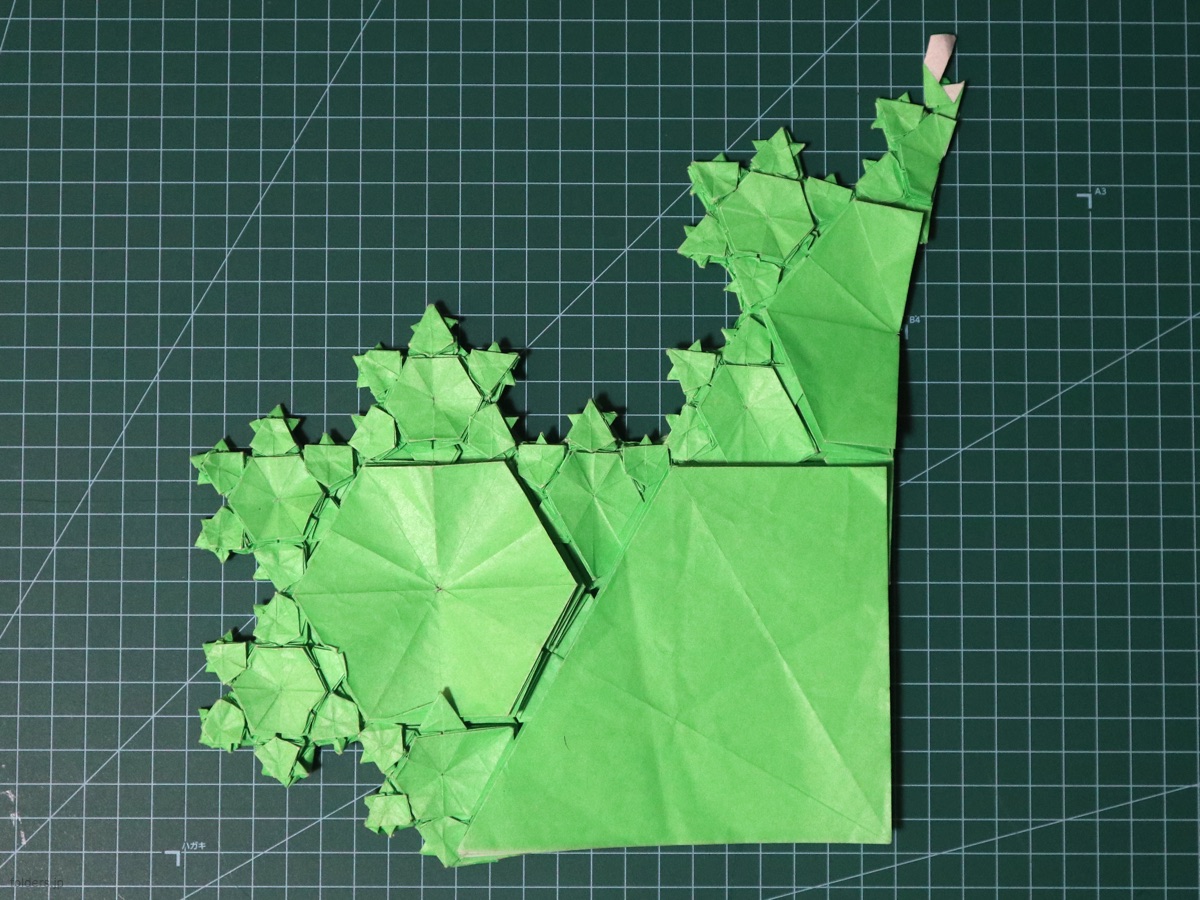
ということで折ってみました。全紙から切り出した六角形の1/4の形の用紙を使用。それでも最終的にはミリ単位の作業になりました。折り手順は大きい方から小さい方へ。いろいろ手順を考えながら折ってみましたが、凹み部分は一気に折るしかなさそうです。
内側の繰り返しについては予想通り問題なし。厚みとサイズさえ気にしなければ何回でも繰り返し可能です。また外側はとりあえず畳めたものの、残念ながら明確なパターン化はできていません。ただ折れること自体はほぼ間違いなさそうなので、階層パターン化が次……というか最後の課題となります。
感想
完成画像を出したX(旧Twitter)のツイートが、意外にも多くのいいねやPV数などを叩き出しました。フラクタルは折り紙としては超不人気分野なのですが、数学系の方からみると案外面白い試みなのかもしれません。
創作の過程を見直してみると、コッホの雪を追っていたら六角ピラミッドが現れたのが、色々な意味でとても面白いと感じました。伏線……という訳ではなく偶然だとは思うのですが、それでも数少ないフラクタル折り紙作品がリンクするというのは面白く、なにより近い構造の作例があるのは、完成への大きな励みとなりました。
最後に、本文でも散々参照している繰り返しとなりますが、階層的な構造、ピラミッドの作例、そしてそもそも「フラクタルを折る」というコンセプトなど、池上牛雄氏の先行研究がいろいろな意味でベースとなっており、これがあったからこその結果であることを改めてお伝えします。未知の分野への果敢な挑戦に、敬意と謝意を。
資料等
超不人気分野のため、ほぼ池上氏のものしかない。
折紙探偵団マガジン67号:展開図 「コッホの雪」(池上牛雄)
折紙探偵団マガジン74号:ローズアップ「フラクタルを折る-その構造と性質-」(池上牛雄)
折紙探偵団マガジン88号:クローズアップ「新しい無限折りの発見」(池上牛雄)
OrigamiUSA The Fold:Diagrams: Fractal Pyramid(池上牛雄)

OrigamiUSA The Fold:「Fractal Origami for Beginners」(池上牛雄)