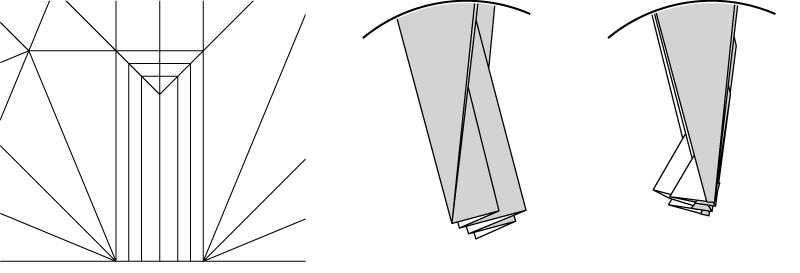
正方形に内接する最大の正五角形の折り出し方。多分車輪の再発明。
正方形から正五角形を折り出す場合、一般的に知られているのは少し誤差のある方法です。また正確な正五角形の場合は、伏見康治先生の著書『折り紙の幾何学』に記載されている方法などが知られています(私の知っている中では一番古そうな出典)。実用としては全く問題ないのですが、ふと最大の大きさの正五角形を折り出す場合はどうなるのかと思い考えてみました。
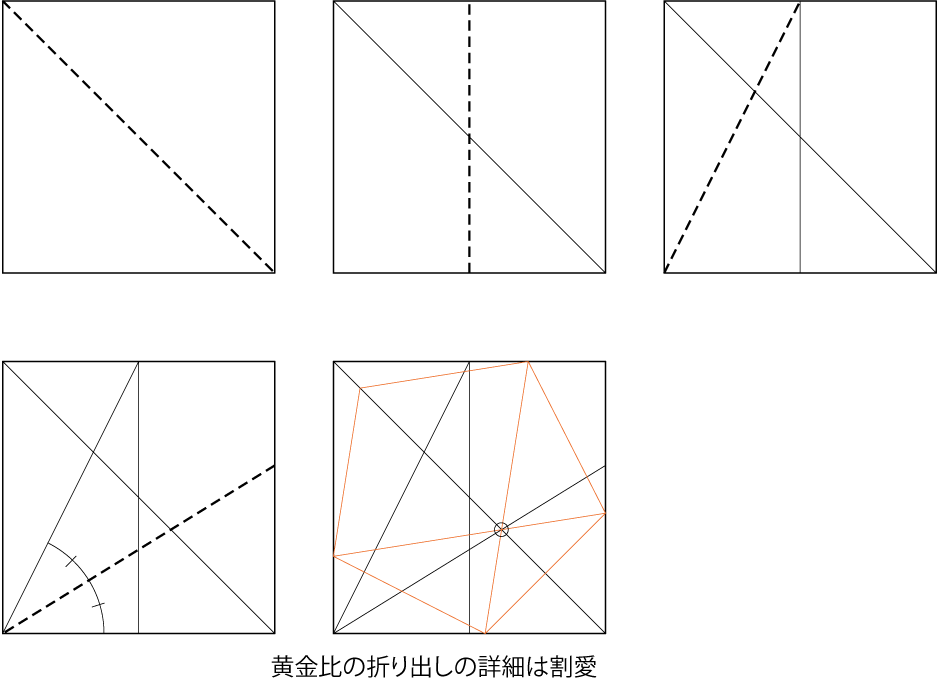
まず、正方形に内接する正五角形は下の図のようになります。

この答え自体は明確なのですが、折り出し方法は意外と難く、正五角形のカドの位置の必要な比率を愚直に折り出すくらいしか思いつきません。 もう少し面白い方法はないかということで、とりあえずカドを結ぶ等の補助線を入れてみます。
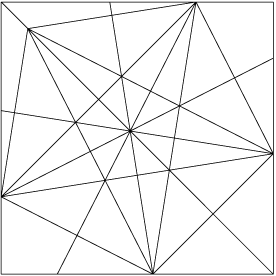
眺めていて気がついたのが、対角線と新しく追加した補助線の交点です。補助線上の交点の位置に注目してみるとわかりやすいのですが、この点は補助線と対角線を黄金比(1:(1+√5)/2)で分割した位置になります。
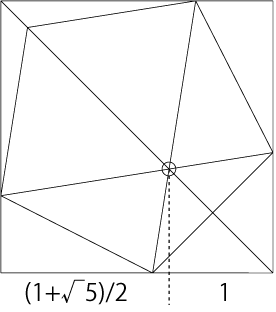
ここまでくればもう出来たも同然(とまずは思っていた)、黄金矩形の対角線と、正方形の対角線の交点として折り出すことができます。
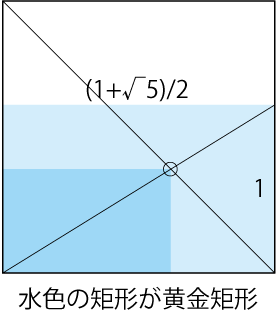
実際の手順は以下のようになります。一切の無駄のない、大変きれいな手順です。
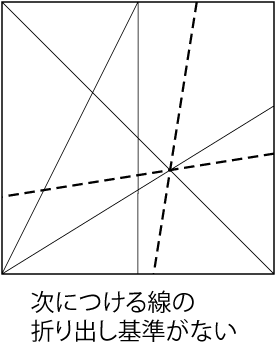
ただし実際に行ってみると、基準点は折り出せたものの、次に折る基準がないことに気がつきます。 せっかくなので最後まで考えてみます。
次に必要なのは正方形の辺から9度傾いた線の折り出しです。方法はいくつかありますが、すでに折り出してある黄金比を利用するのが無駄がなさそうです。ということで、最終的な手順はこちらになります。
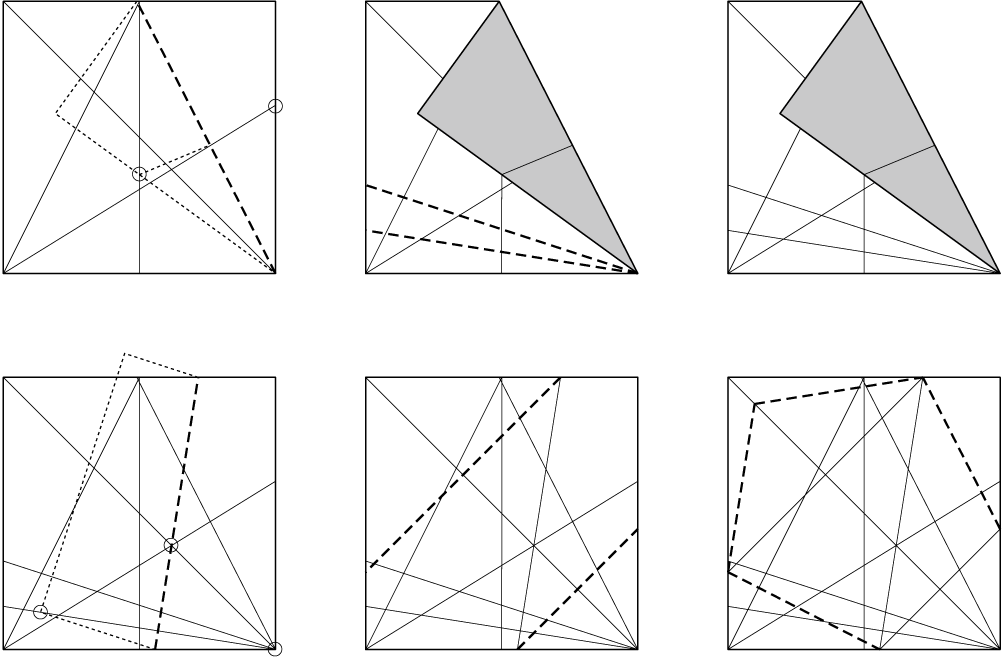
というのを見つけた後で前例を探してみたら、BOSのウェブサイトに、第一回折り紙の科学の国際会議の論文集にてMorassi氏が発表されていたという方法が紹介されていました。まず正五角形の対角線の長さを折り出し、それを必要な位置に移すという手順です。

以上。案外知られていない、実用性は微妙な最大の正五角形の折り出しです。