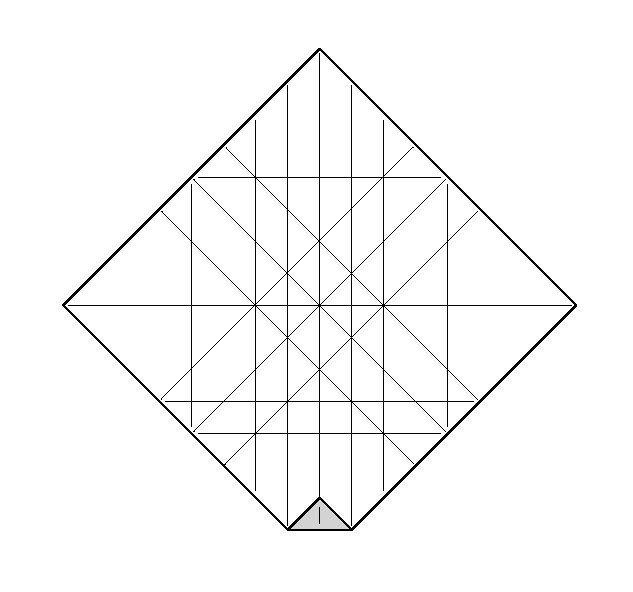
いつもの比の折り出しの話。
1+√2 : 4-2√2 : 1
(賢い人はもっと少ない折り線で求めれるんかなーとか思いつつ…) pic.twitter.com/XjChzCjxxO— 藤田洸 (@NakaOrigami) 2018年8月20日
1+√2 : 4-2√2 : 1
=6-√2。多分折った事のない比率だ。
この手の場合は一辺の長さに対して1を折り出してから、1+√2を出すのがよさそうです。
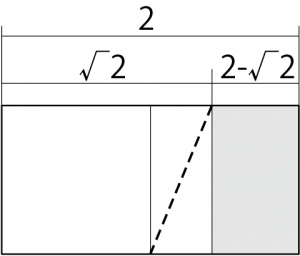
このケースでは4と2-√2に分けるのが恐らく最適解。
意外に思われるかもしれませんが、2-√2はとても折り出しやすい長さです。22.5度の線1本で折り出す事ができます。
という事で折り出し手順。

ポイントは2-√2の折り出しで、見て分かるとおり、2も√2も折り出す必要がありません。
最後に1の幅から22.5度の線で1+√2を折り出せば、完了です。
さて、実はここまでは前置きで(ほぼ最適解であろう答えは出ているのだけれど)、ここからが本題。
もう1つ。6と-√2に分ける場合を考えてみます。
問題は-√2という数値を折り出す事ができるのか?という点なのですが……あまり実用性はないけれど、可能なのです。
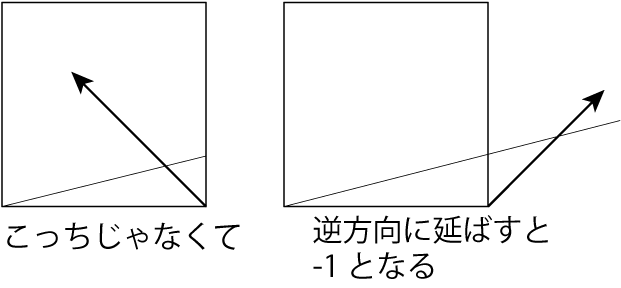
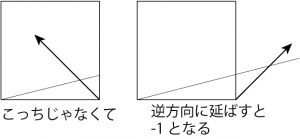
今回使っている折り出し方の場合、カドから2本の線が交差するように内側に向けて基準線をつけるのですが、それを反対側……つまり外側にむけてやるとマイナスの数値を折り出す事ができます。
ただし、紙の外側に折り筋をつけることはできないので、実際には半分の長さなどで折るのがよいでしょう。
分かりやすい例として、3等分の方法を見てみましょう。分割方法は4と-1です。
という事で折り手順はこのようになります。なお実用性はあまりない。この方法が使われている・紹介されているのを私は知りません。
では本番。6と-√2の場合の折り手順です。折り出しやすさの都合上、6:2(=3:1)と-√2:2で折り出しています。
以上、よく考えてみれば当たり前のマイナスの数値の折り出し方法です。活用できるケースは限られているかと思いますが、いざ必要な場合にはとても便利そうです。
折紙探偵団マガジン115号(20期)クローズアップ「22.5度系の比の折り出し」(神谷哲史)
※比の折り出し方法等の解説です。合わせてご覧下さい。