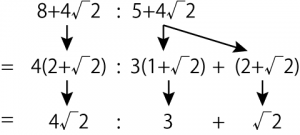折紙探偵団マガジン167号に掲載された豊村高志さんのおおさんしょううお、記事では折り出しやすい近似値を利用していますが、実際はどのような比率なのでしょうか? またどのように折り出せばいいのでしょうか?
※実際に折る時には問題にはならない程度ですが、小さなズレがあります。
比率を求める
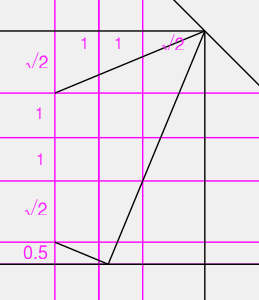
複雑な比率を計る時は、縦横に基準線を加えると分かりやすくなります。
ぜひマガジンの展開図と比べてみて下さい。
内側の部分で数字を取り出します。中略。結果、脚のカドになる点の両側は、
4+2√2:2.5+2√2
となります。2.5ってなんだよ。
数値の約分
0.5を扱い易くするためにまず2倍にします。
8+4√2:5+4√2
それにしても数字が大きい。もう少し分かりやすい数字にできないでしょうか?
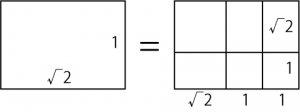
ここで利用するのが、「1+√2:2+√2 = 1:√2」。
ということで、それぞれ1+√2で割ります。つまり、
4(2+√2):3(1+√2)+(2+√2)
=4√2:3+√2
かなりシンプルな数字になりました。
折り出し
とりあえず、合計して1辺全体の長さを求めます。
3+5√2
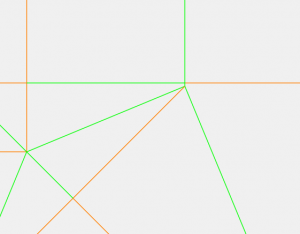
いろいろな可能性が考えられますが、今回については2√2と3+3√2に分けて折り出すのがよさそうです。折り出したい点との相性もいいし。
次、考えやすさののため、全部√2倍します。(必然ではありませんが、√が少ない方が分かりやすいという程度の理由です。)
2√2:3+3√2
=4:6+3√2
折り出しやすそうな数字になってきました。
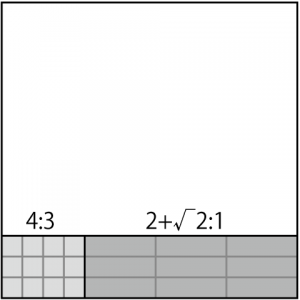
3√2の「3」をどのように折り出すかだけが問題ですが、今回は4:3の長方形を利用して折り出します。
それぞれの比率を横幅、縦幅を3とすると、折り出しに必要な長方形は「4:3」と「3(2+√2):3 = 2+√2:1」で、どちらも簡単に折り出せる比率です。
折り手順
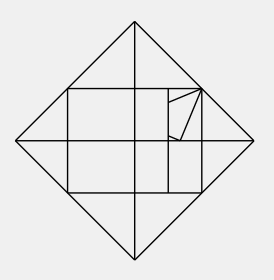
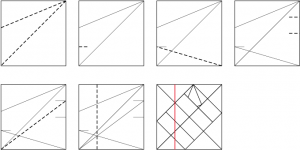
実際の折り手順は以下のようになります。顎になる点が折り出せますね。
以上、使った事のない比率だったので考えてみました。