2010年のメモが案外面白かったので。需要はについては考えない。
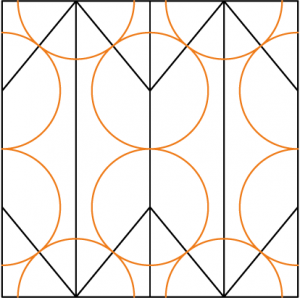
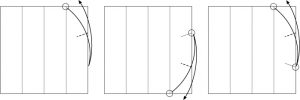
シッポ・マボナさんのアリの構造が面白い。左右の1:2の長方形にそれぞれ6つのカドが詰め込まれているという、サークルパッキングらしい、無駄の無い構造だ。 ただし、折り出しはそう簡単ではない。さて、どう折り出す? というか、折るだけでいけるのか?
sipho mabona ant references? - The Origami Forum
形を見ていると、なんとなく任意角の三等分を思い出すのだが、あまり関係がなさそうだ。そもそも「3等分する角度」か「3等分の起点」が分かればそれがほぼ答えだという事にすぐに気がついた。これは一旦忘れよう。
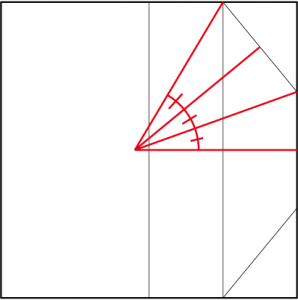
似てはいるんですけどね。
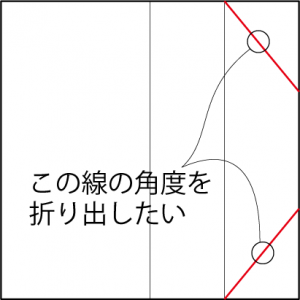
整理しよう。折り出したいのは、横の辺に位置するカドの点、もしくはカドの折り込んである線の角度だ。この場合、どちらかというと角度の方が折り出しやすそうな気がする。紙の横のカドの間隔(カドの長さを1として、この長さを2としておこう)を適当なところに折り出して、それを基準に紙の上下の点を折り出すのがよさそうだ。
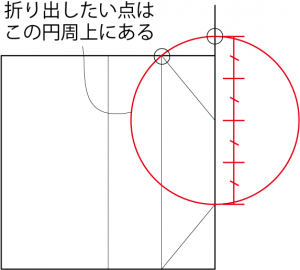
で、あとはこの2の長さの円周上のどこかに上下の辺のカドがある訳だ。 なにか他にもうひとつ基準はないか……ある。
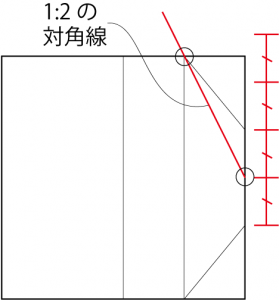
展開図で見た場合、上辺のカドと横の辺の中間点を結ぶ線は、1:2の対角線になっている。これと上記の半径2の円を組み合わせればいい訳だ。
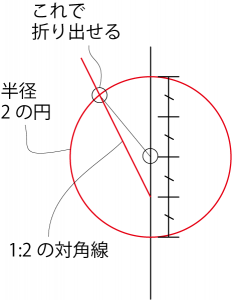
で、実際の手順。効率化してあるけれど、基本的な考え方は上記の基準を利用している。
以上。もっと良い手順があるかもしれないけど、とりあえず折り出せる事は分かったので満足。
2011/11追記。 少し後で、展開図を眺めていて、ふとまったく気がついていなかった解を見つけた。漸近法が使える!!すげえ。これ、手順がループするようなかたちで必要な点を出せば、結構応用できるんじゃないかな。