10年以上前に考えた等分方法についての事と、最近の設計法が実は密接に関連していたという話。
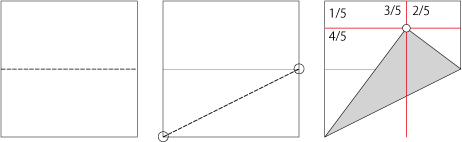
まずは等分方法から。 切っ掛けはこの5等分。
これが何故5等分になるのかといろいろ考えていて、(なぜか)折る線が√5であることに注目、折る線の2乗等分が成立するのではないか?と思いついた。
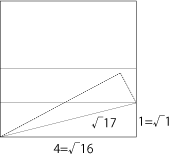
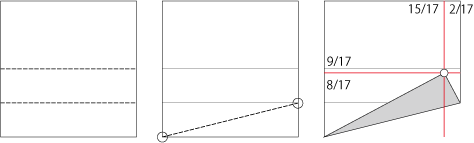
数字を簡単に追ってみた結果、捉え方はいろいろあるにせよそれ自体は問題なさそう。ということで、やってみたのが1:4(√16)の対角線(√17)を使った17等分。
結果は成功。17等分の方法としてはかなり使いやすいのではないだろうか。
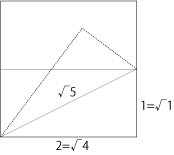
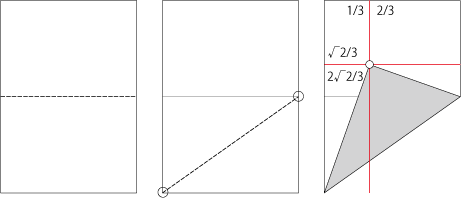
次に3等分。使うのは1:√2:√3の直角三角形、このうち折る線は√3、言い換えると1:√2の長方形の対角線になる。
√が絡むと折り出し辛いけれど、比率によっては素数等分を相当短い手順で折れる。 この段階では「ちょっと面白い等分方法で、実用面では1:√2の長方形を3等分する時に便利そう」というくらいにしか考えていなかった。
で、次が最近の話。
いわゆる神谷パターンや整数比角度系、ラングさんのsterling gridなどがいろいろと研究されているわけなのですが、先週末ごろTwitterでの話題を見ていて、上記の等分方法って実はこれらと密接に関連していたんだなと、いまさら気がついた。
この等分方法は、折ったカドの位置で縦横両方の等分が同時に出来ます。つまり、縦横等分する・カドはその等分グリッドに乗っている上に、整数の対角線ができる……他他数字から実用面までしっかり関連している。
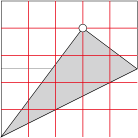
5等分の場合、カドの位置から左側を見てみると3:4:5のいわゆる神谷パターンになる事がわかります。3等分はラングさんのsterling gridとかですね。
そして同時に気がついたのが、恐らく逆もいける。つまりこの等分方法の結果から、なんらかのグリッドが成立する。使いやすさに差はあると思うけれど、少なくとも指定の単位で折り畳める角度のセットが得られる。ベースとなる角度も比率もすぐに分かる。とりあえず整数の対角線だけはいくつか試してみたけれど、見事にピタゴラス数の構造になった。
という感じにいろいろ繋がって腑に落ちたと同時に、神谷パターンを見つけた時に感じた、「絶対他にもあるはず」という直感は当たっていたことを、とりあえず確認できたので満足したというそれだけの話。