しばらく前だけど、面白そうなものを見つけてしまった。
比率の折り出しは趣味なので、せっかくなので勝手に考えてみた。
誰か頭いい人比率出して pic.twitter.com/59TTTv3X8U
— ほんしょい (@honsyoi) 2015, 8月 23
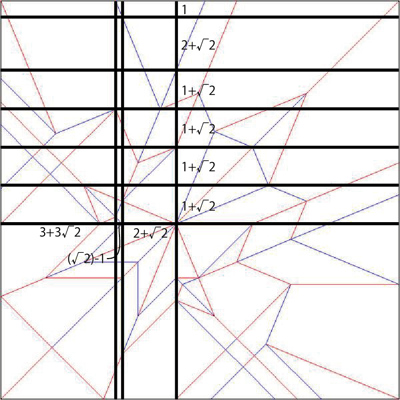
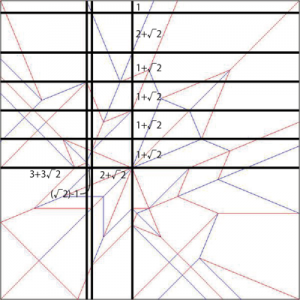
確かに難しい。さすがに そのままではカウントすら難しいので、縦横にいくつか補助線を入れてみる。
※引用元:ほんしょい (@honsyoi)@twitter
これで数えやすくなった。11+10√2だ。約分すると9+√2になる。
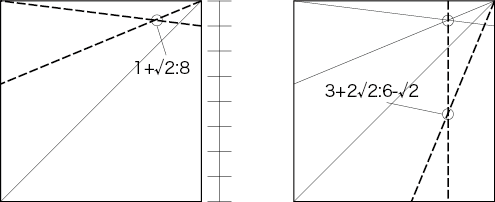
折り出し自体は、8と1+√2に分ければ簡単に出せる。
ただし、出来れば折り出したいのは中心付近の点なので、ここからどうにか結果を3+2√2:6-√2にしたい。
ここで注目すべきは3+2√2で、実はこの数字は1+√2の2乗である。そして1+√2は22.5度を使えば簡単に折り出せるので、意外と使いやすい数字なのだ。
さらに8:1+√2という比の折り出しで元となる側の1+√2も用意できる。よし、繋がった。
という事で、折り出し手順。
分かりやすさのため1:8を使っているけれど、角度が浅すぎてずれやすいので、実際に折るなら1:4と2:1+√2を使う方が良いと思う。